Le moteur Stirling
Ce site appartient au réseau de sites relatifs aux moteurs à air chaud
Ce site appartient au réseau de sites relatifs aux moteurs à air chaud
Dans sa description la plus simple, le moteur Stirling est constitué d'un cylindre renfermant du gaz
et d'un piston récupérant l'énergie mécanique. Cette page propose de découvrir le principe de fonctionnement
de ce moteur. Ceci se fait progressivement en étudiant les étapes suivantes :
- les quatre phases élémentaires
- le rôle du déplaceur
- le diagramme Pression-Volume et le rendement du cycle
Première observation : le gaz utilisé est enfermé, c'est toujours le même qui est mis à contribution. Autre
caractéristique : l'énergie est fournie à l'extérieur du cylindre, d'où les appellations "moteur à air
chaud" ou "moteur à combustion externe" que l'on peut lire parfois.
Le cycle thermodynamique du moteur Stirling est dans son principe très simple : il comprend 4 phases pendant lesquelles le gaz utilisé subit les transformations suivantes :
Le brûleur (la source chaude) cède de l'énergie thermique. On s'imagine aisément que la pression et la température du gaz augmentent durant cette phase.
Le volume s'accroît alors que la pression diminue. C'est pendant cette transformation que l'énergie motrice est produite.
L'eau projetée (la source froide) récupère de l'énergie thermique. La température et la pression diminuent pendant cette phase.
La pression du gaz augmente au fur et à mesure que son volume diminue. On doit fournir de l'énergie mécanique au gaz pendant cette période.
On peut voir ci-dessous l'enchaînement de ces différentes phases.
La réalisation d'un moteur tel que celui décrit ci-dessus poserait des difficultés : allumer le brûleur,
l'éteindre, asperger puis arrêter le refroidissement, chocs thermiques successifs....
C'est pourquoi on va introduire un artifice apportant des solutions à ces problèmes : le déplaceur. Ce
dernier ne modifie ni la pression ni le volume du gaz, mais l'oblige à se situer soit vers la source chaude
située en partie supérieure, soit vers la source froide située en partie inférieure.
Explications grâce à des dessins :
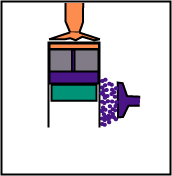
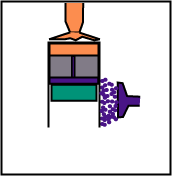
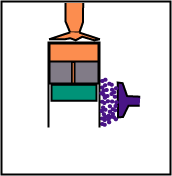
Le volume reste constant, mais le déplaceur, en descendant, chasse le gaz de la partie basse (froide) vers la partie haute (chaude).
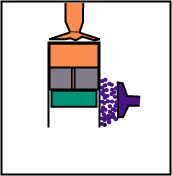
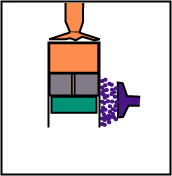
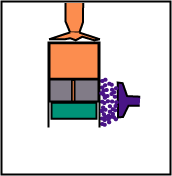
Le déplaceur suit le piston moteur au cours de la détente pour que le gaz reste en contact uniquement avec la source chaude.
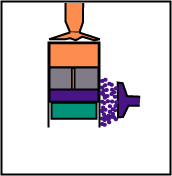
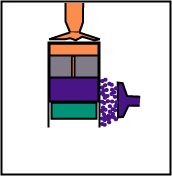
Le volume reste constant, mais le déplaceur, en montant, fait passer le gaz de la partie haute (chaude) à la partie basse (froide).
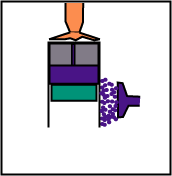
Le déplaceur, au cours de la compression, reste en partie supérieure pour que le gaz reste en contact uniquement avec la source froide.
Le cycle complet est montré ci-dessous. Ce moteur s'appelle le le moteur bêta, son fonctionnement est étudié de façon plus approfondie sur ce site.
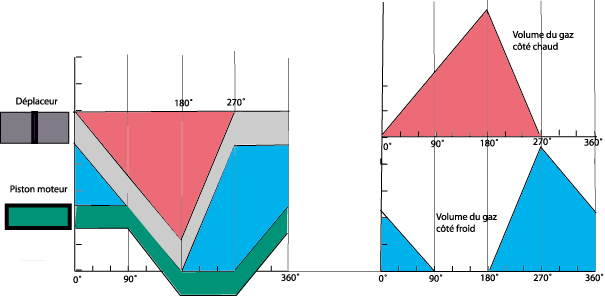
Sur le diagramme ci-dessus, on peut voir :
- la variation du volume chaud en partie haute au cours du cycle (zone rouge).
- la variation du volume froid en partie basse, entre déplaceur et piston moteur, au cours du cycle (zone bleue).
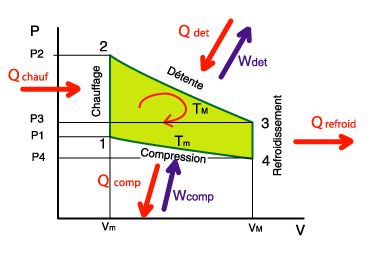
Le principe de fonctionnement, exposé ci-dessus, peut se représenter sur un schéma appelé "diagramme Pression-Volume" ou diagramme (P,V).
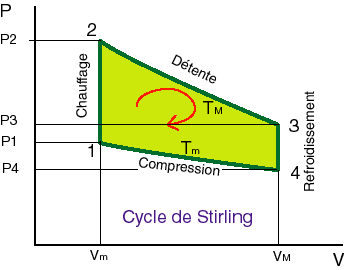
Sur ce diagramme, on voit aisément les quatre phases détaillées plus haut en images, en n'oubliant pas que
détente et compression se font à températures constantes (Tmax et Tmin).
NB : les températures T sont exprimées en Kelvin (rajouter 273 à la température Celsius)
L'aire colorée comprise entre les quatre segments décrivant le cycle est représentative du travail recueilli
au cours d'un cycle.
La démonstration est apportée ci-après.
A un instant donné, la force qui s'exerce sur le piston est F = S x P où S est la surface du piston et P
la pression instantanée.
Le travail élémentaire fourni au cours d'un temps court "dt" est égal à la force instantanée multipliée
par le déplacement "dy"du piston au cours de ce laps de temps "dt".
dW = F x dy
ou
dW = S x P x dy
ou, si on remarque que S x dy = dV , variation de volume au cours du laps de temps "dt"
dW = P x dV
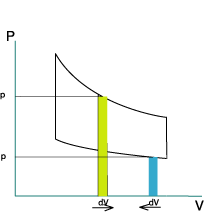
Sur le diagramme(P,V) cette dernière expression n'est rien d'autres que la surface élémentaire située sous
chaque courbe. Voir ci-contre.
Le travail est positif sous la courbe de détente car dV>0. Le travail est négatif sous la courbe de
compression car dV<0.
Le travail résultant au cours d'un cycle est donc représenté par la surface sous la courbe de détente
diminuée de la surface sous la courbe de compression. C'est donc la surface comprise entre les courbes. cqfd !
Le rendement du moteur est égal au rapport entre l'énergie mécanique nette Wnet
effectivement récupérée et l'energie calorifique Qtotale qu'il est nécessaire
de fournir au moteur. Cette dernière est fournie au cours du chauffage isochore et au cours de la
détente isotherme.
Si on regarde le diagramme ci-contre, on peut écrire :
Wnet = Wdet + Wcomp
Comme il est expliqué ci-dessus, Wcomp sera négatif quand on le calculera.
Qtotale = Qchauf + Qdet
Ce travail Wnet est égal à la somme du travail récupéré au cours de la détente (travail
positif) et du travail qu'il est nécessaire de fournir au cours de la compression du gaz (travail négatif) :
Wnet = Wdet + Wcomp
Wnet = ∫det PdV + ∫comp PdV
avec P = nRT / V
ce qui donne :
Wnet = ∫det (nRTmax / V) dV + ∫comp (nRTmin / V) dV
Wnet = nR (Tmax - Tmin) ln Vmax / Vmin
Au cours d'une détente isotherme, la quantité de chaleur fournie au système est égale au travail
récupéré au cours de cette même phase :
Qdet = ∫det PdV
Qdet = nR Tmax ln Vmax / Vmin
Au cours du chauffage isochore, il a fallu fournir l'énergie suivante :
Qchauf = nCv (Tmax - Tmin)
où Cv est la chaleur molaire du gaz considéré pour un chauffage, à volume constant, d'une
température Tmin à une température Tmax.
La quantité totale d'énergie calorifique fournie est donc de :
Qtotale = nCv (Tmax - Tmin) + nR Tmax ln
Vmax / Vmin
On peut donc écrire la valeur du rendement d'un cycle de Stirling :
Rendement d'un cycle de Stirling :
η = [R (Tmax - Tmin) ln Vmax / Vmin]
/ [Cv (Tmax - Tmin) + R Tmax ln Vmax / Vmin]
Le rendement du cycle de Stirling est égal au rendement du cycle de Carnot.
L'affirmation barrée ci-dessus, qu'on trouve trop souvent, est fausse si on a suivi le raisonnement exposé
dans ce chapitre. En effet, le cycle de Carnot a pour valeur : ηCarnot = 1 - Tmin
/ Tmax ce qui est différent de la formule propre au rendement du cycle de Stirling.
Par contre, si on suppose que l'énergie nécessaire au réchauffage isochore est entièrement récupérée au
cours du refroidissement isochore, c'est le rôle du régénérateur étudié dans la page
"Régénérateur", alors l'efficacité du moteur Stirling sera égale au rendement d'une machine de Carnot,
jamais conçue, ayant les mêmes températures extrêmes de fonctionnement.
En effet, dans l'équation définissant le rendement η, le terme correspondant à l'énergie utile au
chauffage isochore Cv (Tmax - Tmin) disparaît.
L'expression du rendement du moteur devient :
η = [R (Tmax - Tmin) ln Vmax / Vmin]
/ R Tmax ln Vmax / Vmin
ou, après simplification :
η = (Tmax - Tmin) / Tmax
ou encore :
Rendement d'un moteur Stirling avec un régénérateur :
η = 1 - Tmin / Tmax = ηCarnot
Maintenant, on peut affirmer que le rendement d'un moteur Stirling est égal à celui du cycle de Carnot. Dans la réalité, l'hypothèse faite, récupérer totalement la chaleur du refroidissement isochore pour la restituer au cours du chauffage isochore, est très optimiste pour ne pas dire impossible à réaliser sur un plan pratique. Il faudrait pour cela que le régénérateur ait une efficacité de 100%. Concevoir un tel échangeur est une vrai gageure.
Conclusion : on peut dire que le génie de Robert Stirling ne réside pas exclusivement dans le fait d'avoir imaginé le cycle portant son nom, mais plutôt dans l'invention du régénérateur (ou économiseur) qui en améliore singulièrement le rendement !
Ce site a été conçu et réalisé par Pierre Gras. Merci à toutes les personnes qui ont apporté leurs contributions : articles, photos, vidéos, feuilles de calcul... L'auteur est ouvert à toute suggestion permettant d'améliorer ce site pour le bonheur de tous. Enfin, un grand merci à Robert Stirling !
Le site "moteurstirling.com" par Pierre Gras est mis à disposition selon les termes de la licence Creative Commons
.
Ce site respecte les normes relatives aux langages XHTML et CSS. Pour en profiter au mieux, utilisez un logiciel récent tel que Firefox, Chrome, Safari, Opera... qui ,eux-aussi, se conforment à ces normes.
